Algorithms for smoothing step-wise linear paths down to bounded curvature
22 Feb 2022 | all notes
For a project I have been looking for an algorithm that takes a non-intersecting 2d step-wise linear path (actually the outer ring of a polygon) and smoothes it down (numerically) to a path that would make for a non-jittery camera movement along it. The two basic constraints are that:
- the resulting path should not exceed some set maximum local curvature – assuming a constant speed traversal of the path, this is equivalent to a bounded angular acceleration constraint
- the resulting path should contain as many points of the original path as possible
Constraint 2 is worth elaborating on: in particular it does not mean that all vertices of the original path need to be maintained. It is in fact at the corner/turning points where dropping/interpolating/adding new points will be necessary to achieve the ‘smoothing off’ required for a particular curvature. On the contrary, it is exactly the straight stretches along the longest edges of the original trajectory that should be maintained as closely as possible.
Despite a plethora of line smoothing algorithms I have been unable to find one that satisfies these two basic requirements. My impression is that this is because existing algorithms can be split into three groups, each focussed on different constraints/criteria based on their practical use case/application (and that, unfortunately, the creation of smooth simplified camera trajectories is not one of them).
Robotic path planning
Most current research on path smoothing that I found comes from the literature on path planning for autonomous robots (often with some obstacle avoidance thrown in). Algorithms in this domain often take curvature/acceleration constraints into account, and are consequently often based on analytic representations (Bezier curves etc). One downside is that in path planning the vertices of the original path are typically considered to be “critical points” that need to be hit exactly by the path, while other points along the trajectory which can be deviated from quite freely. Apart from the complexity of the algorithms, their goal – hitting a few points exactly at all costs while moving freely in other areas – is exactly the opposite of my constraint, so I haven’t found anything really suitable in this domain.
(There is another less popular approach in this area, based on fitting a path through a ‘corridor’ given be linear boundaries on either side, which sounds somewhat more suitable.)
Cartographic line simplification
Line simplification is a classic problem in cartography, where the goal is to simplify stepwise linear paths that are measured at a small scale to derive a large scale representation of them which maintains their basic outline. Several different algorithms which focus on preserving different aspects of the paths are known (see the comparison below, courtesy of ArcGIS), most of them fast and strictly numeric.
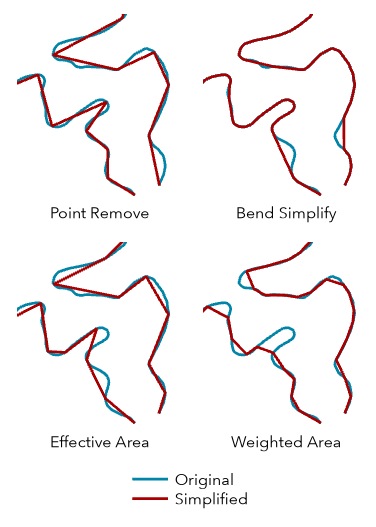
None of these algorithms seem suitable for my purposes, mainly for two reasons:
- they only remove vertices, which results in smoother lines when viewed from the larger scale, but no actual smoothing of corners happens at the original scale
- most of the algorithms are more likely to preserve extreme turns that are most defining/characteristic of the paths, which is in a way the opposite of what I am looking for
Line smoothing heuristics
Most appropriate for my problem seem to be simple numerical heuristics for line or polygon smoothing, such as Chaikin’s corner cutting algorithm. Two promising improved versions of corner cutting with trapezoidal augmentation (CCA1 and CCA2) sound promising, however they both unneccessarily shift long straight edges. The general problem with these algorithms is that they greedily add new vertices, which means that they can’t recover from attempts at smoothing down corners which can’t be smoothed down except by completely removing entire vertices/edges. In terms of their parameterisation (cutting/smoothing at fixed proportional offsets of each edge) they generally seem ill-suited to paths with highly variable edge lengths.
There is some research on the smoothness of the limiting curve of corner cutting algorithms. Being able to detect corners which are impossible to smooth down to a given curvature (either beforehand or during runtime) could be used to inform dropping of vertices, which would then allow the simple heuristic to produce a valid smoothed curve.