Perform one or more Mantel permutation tests.

Perform correlation tests between pairs of distance matrices. The Mantel test is different from classical correlation tests (such as those implemented by cor.test) in that the null distribution (and significance level) are obtained through randomisation. The null distribution is generated by shuffling the locations (matrix rows and columns) of one of the matrices to calculate an empirical null distribution for the given data set.

mantel.test(x, y, ...)

# S3 method for default
mantel.test(x, y, plot = FALSE, method = c("spearman",
  "kendall", "pearson"), trials = 9999, omitzerodistances = FALSE, ...)

# S3 method for formula
mantel.test(x, y, groups = NULL,
  stringdistfun = utils::adist, meaningdistfun = hammingdists, ...)

# S3 method for list
mantel.test(x, y, plot = FALSE, ...)

# S3 method for mantel
plot(x, xlab = "generation", ...)

Arguments

x	a formula, distance matrix, or list of distance matrices (see below)
y	a data frame, distance matrix, or list of distance matrices of the same length as `x`
...	further arguments which are passed on to the default method (in particular `plot`, `method`, `trials` and `omitzerodistances`)
plot	logical: immediately produce a plot of the test results (default: `FALSE`)
method	correlation coefficient to be computed. Passed on to `cor`, so one of `"spearman"`, `"kendall"`, or, inadvisable in the case of ties: `"pearson"`. Following Dietz (1983), `"spearman"` is used as a default that is both powerful and robust across different distance measures.
trials	integer: maximum number of random permutations to be computed (see Details).
omitzerodistances	logical: if `TRUE`, the calculation of the correlation coefficient omits pairs of off-diagonal cells which contain a 0 in the second distance matrix argument. (For the formula interface, this is the matrix which specifies the meaning distances.)
groups	when `x` is a formula: column name by which the data in `y` is split into separate data sets to run several Mantel tests on
stringdistfun	when `x` is a formula: edit distance function used to compute the distance matrix from the specified string column. Supports any edit distance function that returns a distance matrix from a vector or list of character strings. Default is Levenshtein distance (`adist`), other options from this package include `normalisedlevenshteindists()` and `orderinsensitivedists()`.
meaningdistfun	when `x` is a formula: meaning distance function used to compute the distance matrix from the specified meaning columns. Defaults to Hamming distances between meanings (`hammingdists()`), custom meaning functions can be created easily using `wrap.meaningdistfunction()`.
xlab	the x axis label used when plotting the result of several Mantel tests next to each other

Value

A dataframe of class mantel, with one row per Mantel test carried out, containing the following columns:

method: Character string: type of correlation coefficient used
statistic: The veridical correlation coefficient between the entries in the two distance matrices
rsample: A list of correlation coefficients calculated from the permutations of the input matrices
mean: Average correlation coefficient produced by the permutations
sd: Standard deviation of the sampled correlation coefficients
p.value: Empirical p-value computed from the Mantel test: let ngreater be the number of correlation coefficients in rsample greater than or equal to statistic, then p.value is (ngreater+1)/(length(rsample)+1
p.approx: The theoretical p-value that would correspond to the standard z score as calculated above.
is.unique.max: Logical, TRUE iff the veridical correlation coefficient is greater than any of the coefficients calculated for the permutations. If this is true, then p.value == 1 / (length(rsample)+1)

Multiple mantel objects can easily be combined by calling rbind(test1, test2, ...).

Details

If the number of possible permutations of the matrices is reasonably close to the number of permutations specified by the trials parameter, a deterministic enumeration of all the permutations will be carried out instead of random sampling: such a deterministic test will return an exact p-value.

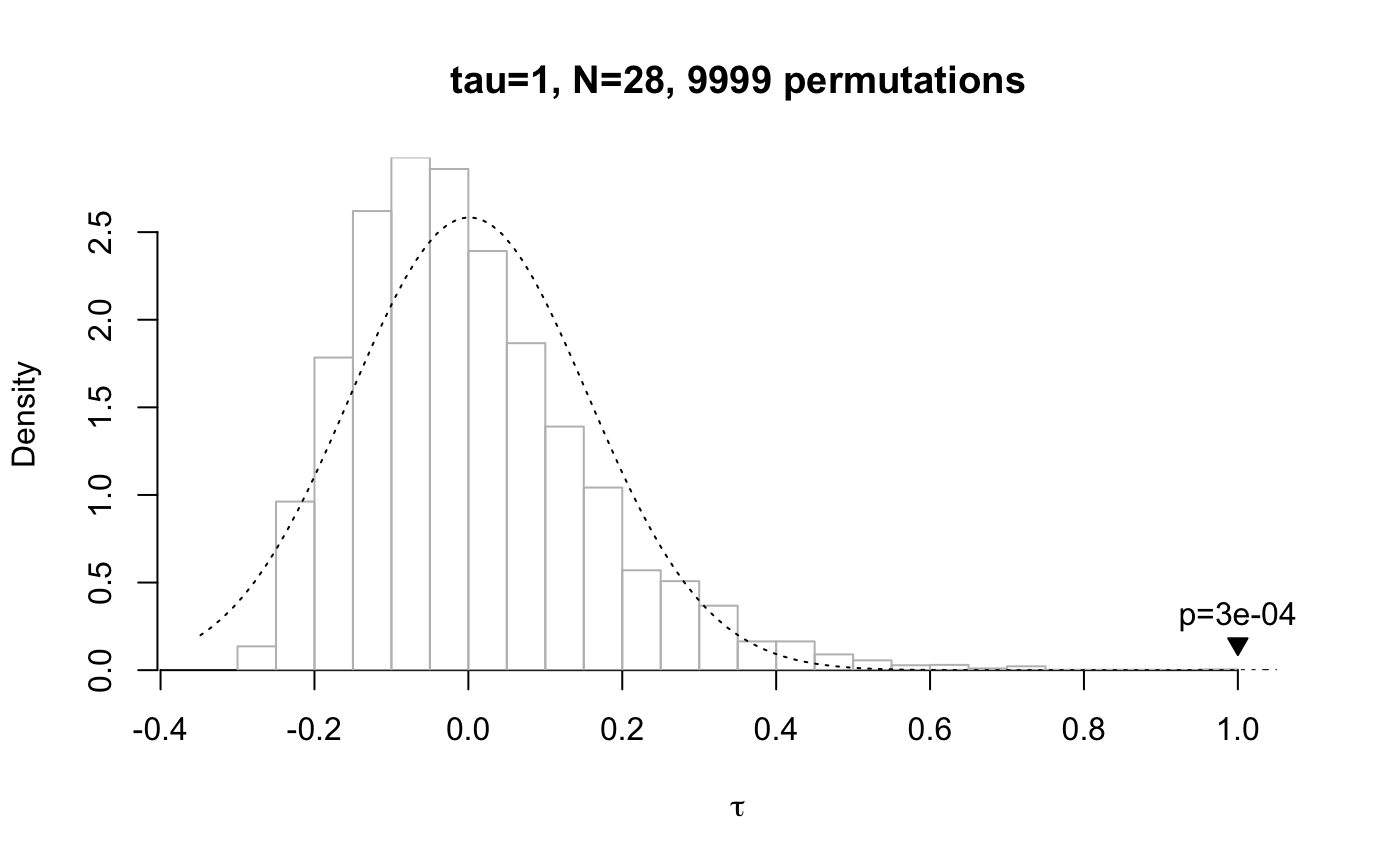
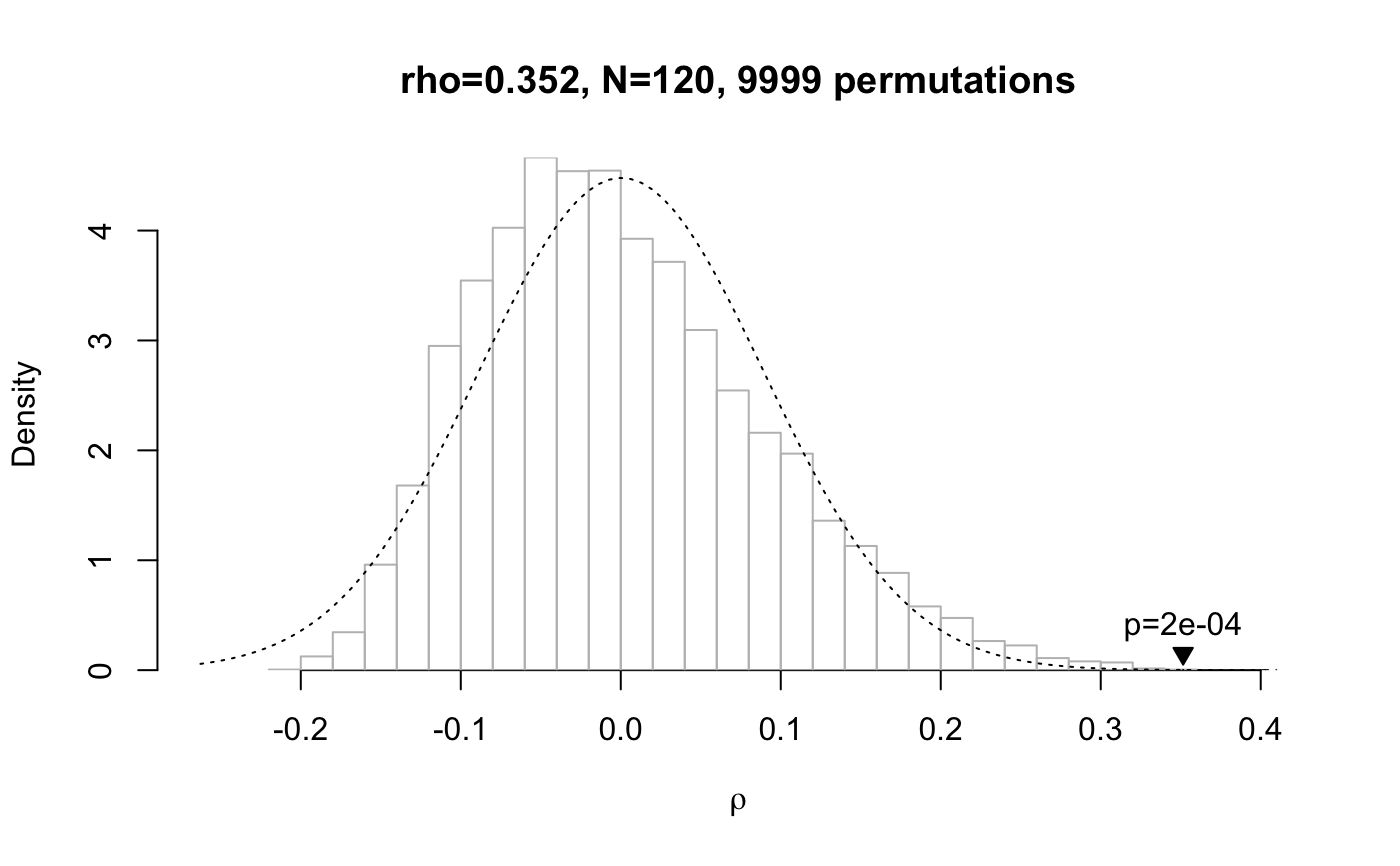
plot() called on a data frame of class mantel plots a visualisation of the test results (in particular, the distribution of the permutated samples against the veridical correlation coefficient). If the veridical correlation coefficient is plotted in blue it means that it was higher than all other coefficients generated by random permutations of the data. When the argument contains the result of more than one Mantel tests, a side-by-side boxplot visualisation shows the mean and standard deviation of the randomised samples (see examples). Additional parameters ... to plot() are passed on to plot.default.

Methods (by class)

default: Perform Mantel correlation test on two distance matrices. The distance matrices can either be of type dist, plain R matrices or any object that can be interpreted by check.dist. The order of the two matrices does not matter unless omitzerodistances = TRUE, in which case cells with a 0 in the second matrix are omitted from the calculation of the correlation coefficient. For consistency it is therefore recommended to always pass the string distance matrix first, meaning distance matrix second.
formula: This function can be called with raw experimental result data frames, distance matrix calculation is taken care of internally. x is a formula of the type s ~ m1 + m2 + ... where s is the column name of the character strings in data frame or matrix y, while m1 etc. are the column names specifying the different meaning dimensions. To calculate the respective distances, the function stringdistfun is applied to the strings, meaningdistfun to the meaning columns.
list: When x is a list of distance matrices, and y is either a single distance matrix or a list of distance matrices the same length as x: runs a Mantel test for every pairwise combination of distance matrices in x and y and returns a mantel object with as many rows.

References

Dietz, E. J. 1983 “Permutation Tests for Association Between Two Distance Matrices.” Systematic Biology 32 (1): 21-–26. https://doi.org/10.1093/sysbio/32.1.21.

North, B. V., D. Curtis and P. C. Sham. 2002 “A Note on the Calculation of Empirical P Values from Monte Carlo Procedures.” The American Journal of Human Genetics 71 (2): 439-–41. https://doi.org/10.1086/341527.

Examples

# small distance matrix, Mantel test run deterministically
mantel.test(dist(1:7), dist(1:7))
#> Permutation space is small, enumerating all 5040 possible permutations.
#> Mantel permutation test (method: spearman)
#> r = 1, N = 21
#> 5040 permutations, mean = -8.02e-19, sd = 0.224
#> p (exact) = 0.000595
#> 


# run test on smallest distance matrix which requires a random
# permutation test, and plot it
plot(mantel.test(dist(1:8), dist(1:8), method="kendall"))

# 2x2x2x2 design
mantel.test(hammingdists(enumerate.meaningcombinations(c(2, 2, 2, 2))),
  dist(1:16), plot=TRUE)
#> Mantel permutation test (method: spearman)
#> r = 0.352, N = 120
#> 9999 permutations, mean = 0.00031, sd = 0.0891
#> p (empirical) = 2e-04
#> 

# using the formula interface in combination with a data frame:
print(data <- cbind(word=c("aa", "ab", "ba", "bb"),
  enumerate.meaningcombinations(c(2, 2))))
#>      word Var2 Var1
#> [1,] "aa" "1"  "3" 
#> [2,] "ab" "1"  "4" 
#> [3,] "ba" "2"  "3" 
#> [4,] "bb" "2"  "4" 

mantel.test(word ~ Var1 + Var2, data)
#> Permutation space is small, enumerating all 24 possible permutations.
#> Mantel permutation test (method: spearman)
#> r = 1, N = 6
#> 24 permutations, mean = 0, sd = 0.722
#> p (exact) = 0.36
#> 

# pass a list of distance matrices as the first argument, but just one
# distance matrix as the second argument: this runs separate tests on
# the pairwise combinations of the first and second argument
result <- mantel.test(list(dist(1:8), dist(sample(8:1)), dist(runif(8))),
  hammingdists(enumerate.meaningcombinations(c(2, 2, 2))))

# print the result of the three independently run permutation tests
print(result)
#> Group '1':
#> Mantel permutation test (method: spearman)
#> r = 0.316, N = 28
#> 9999 permutations, mean = -0.00248, sd = 0.191
#> p (empirical) = 0.0477
#> 
#> Group '2':
#> Mantel permutation test (method: spearman)
#> r = 0.068, N = 28
#> 9999 permutations, mean = -0.00263, sd = 0.193
#> p (empirical) = 0.365
#> 
#> Group '3':
#> Mantel permutation test (method: spearman)
#> r = -0.0931, N = 28
#> 9999 permutations, mean = 0.00111, sd = 0.198
#> p (empirical) = 0.617
#> 

# show the three test results in one plot
plot(result, xlab="group")